DP

操作演示

模型介绍

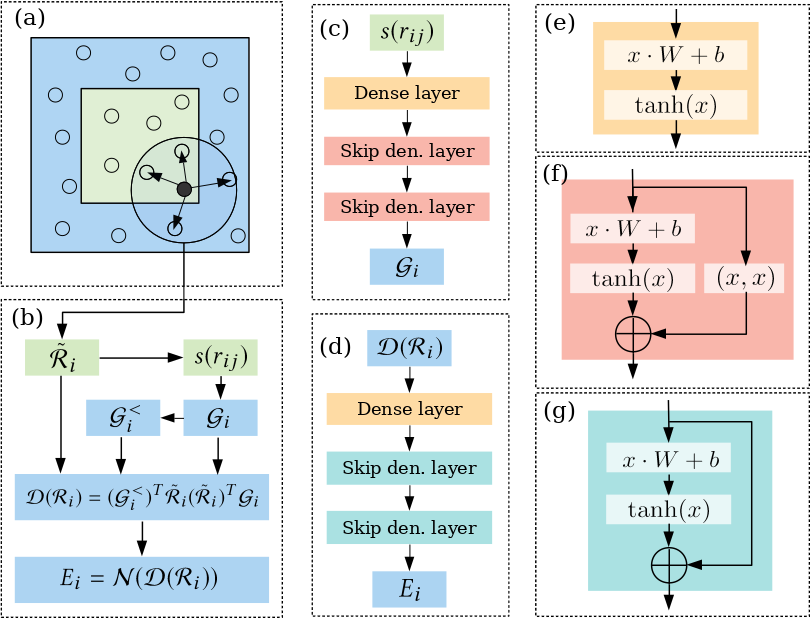
DP 模型请参考文献：

• [SC’20] Weile Jia, Han Wang, Mohan Chen, Denghui Lu, Lin Lin, Roberto Car, E Weinan, Linfeng Zhang*, "Pushing the Limit of Molecular Dynamics with Ab Initio Accuracy to 100 Million Atoms with Machine Learning," SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, 2020, pp. 1-14, doi: 10.1109/SC41405.2020.00009.(CCF-A)(Gordon Bell Prize)

• Han Wang, Linfeng Zhang, Jiequn Han, and Weinan E. "DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics." Computer Physics Communications 228 (2018): 178-184. doi:10.1016/j.cpc.2018.03.016

• Zhang L, Han J, Wang H, et al. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems[J]. Advances in neural information processing systems, 2018, 31.

• Lu D, Jiang W, Chen Y, et al. DP compress: A model compression scheme for generating efficient deep potential models[J]. Journal of chemical theory and computation, 2022, 18(9): 5559-5567.

type embedding

由于 DP 模型的 Embedding Net 数目是元素类型数目$N$的$N^2$倍。一方面，当体系中元素类型较多时制约了模型的训练速度，以及推理速度。另一方面，这也制约了 DP 模型在通用大模型方面的潜力。考虑到$N^2$个 Embedding net 其实隐含了对元素类型的编码，因此我们通过调整$S_{ij}$，将元素类型的物理属性信息与$S_{ij}$做拼接，则只需要一个 Embedding net 即可达到与$N^2$相似效果。

对于$S_{ij}$，$i$为中心原子，这里将$j$对应的元素类型的物理属性与$S_{ij}$做拼接，组成一个长度为 1+物理属性数量的 Vector 送入 Embedding Net。在我们五元合金(钌、铑、铱、钯、镍)数据集以及LiGePS 四元数据集(1200K)的测试中，基于这种 Type embedding 方法的 DP 模型，能够在达到或者超过标准的 DP 模型预测精度的同时，对训练时间减少 27%，详细结果见性能测试。

使用方法

用户只需要在控制训练的 json 文件中加入$type\_embedding$参数，即可开启模型训练，将使用默认物理属性训练，参见项目案例 example/LiGePS/ligeps.json。

{
  "type_embedding": true
}

用户也可以在该 Json 文件的 model 参数 中指定所需要的物理属性。

性能测试

精度

五元合金混合数据集(9486 个构型)下，Type embedding 方法相对于标准的 DP 模型在验证集上的预测精度对比:

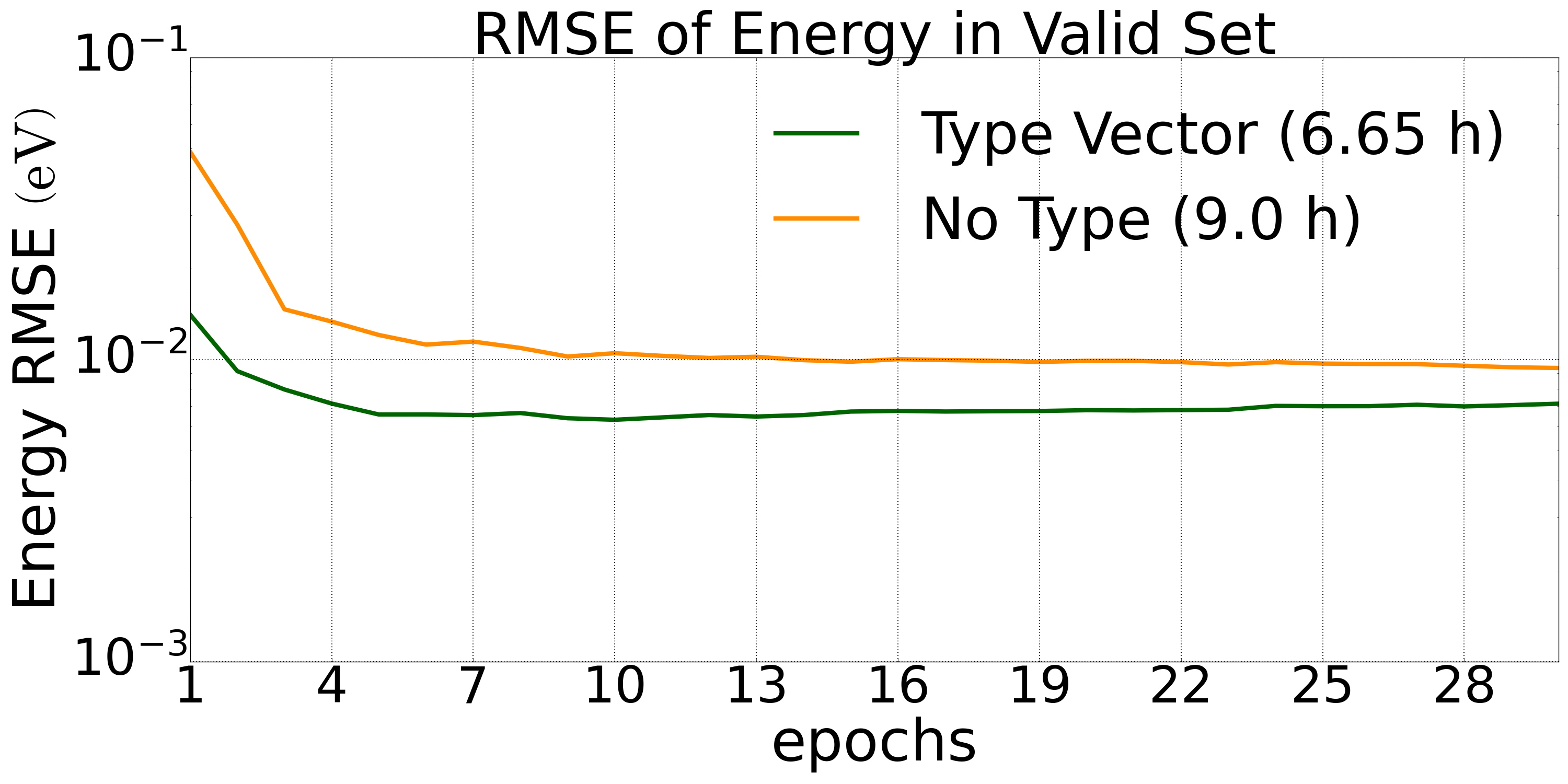图1: 五元合金体系验证集上的能量误差下降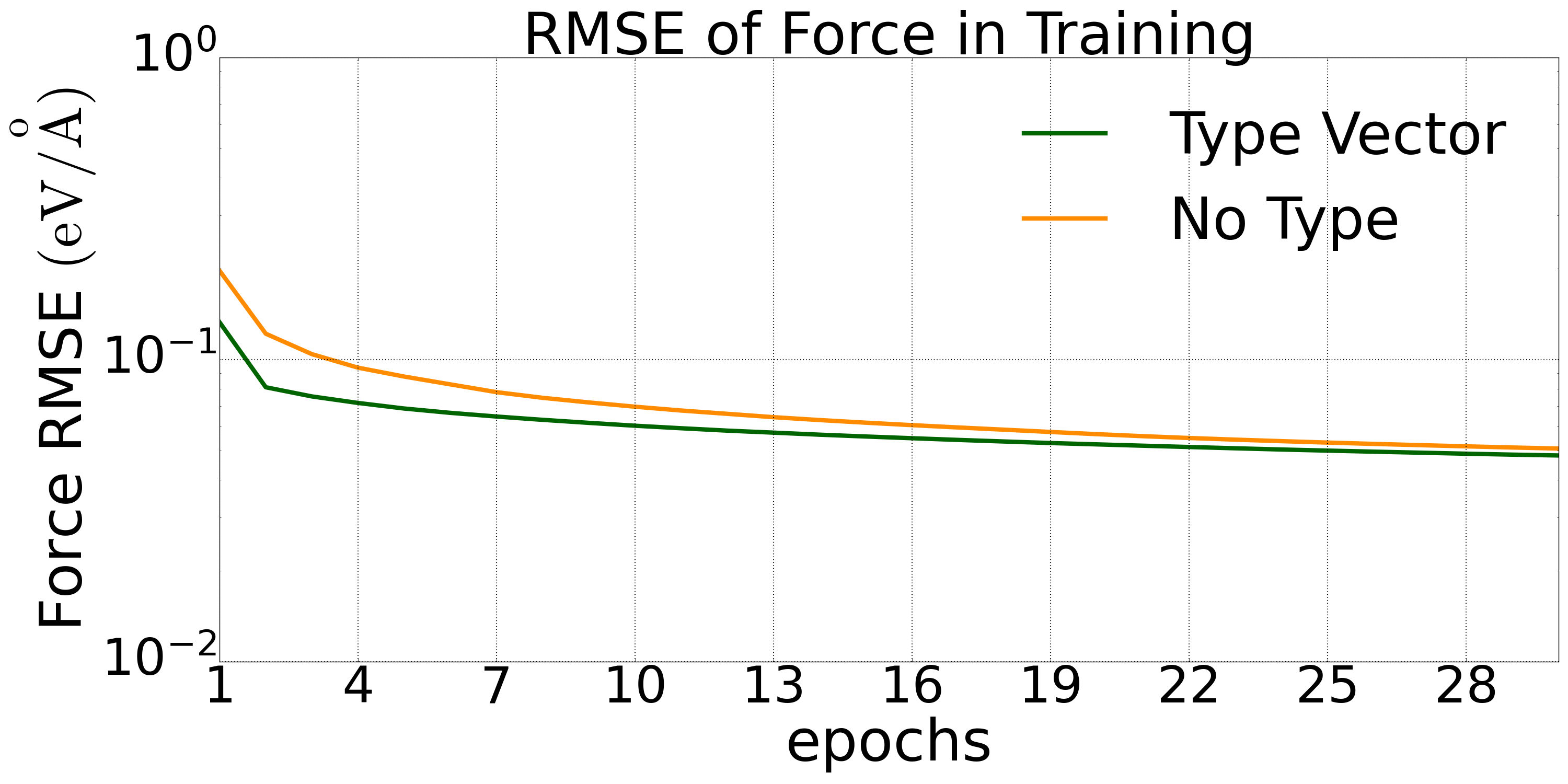

图2: 五元合金体系验证集上的力误差下降

四元 LiGePS 构型的数据集（10000 个构型 1200K）下 Type embedding 方法相对于标准的 DP 模型在验证集上的预测精度对比:

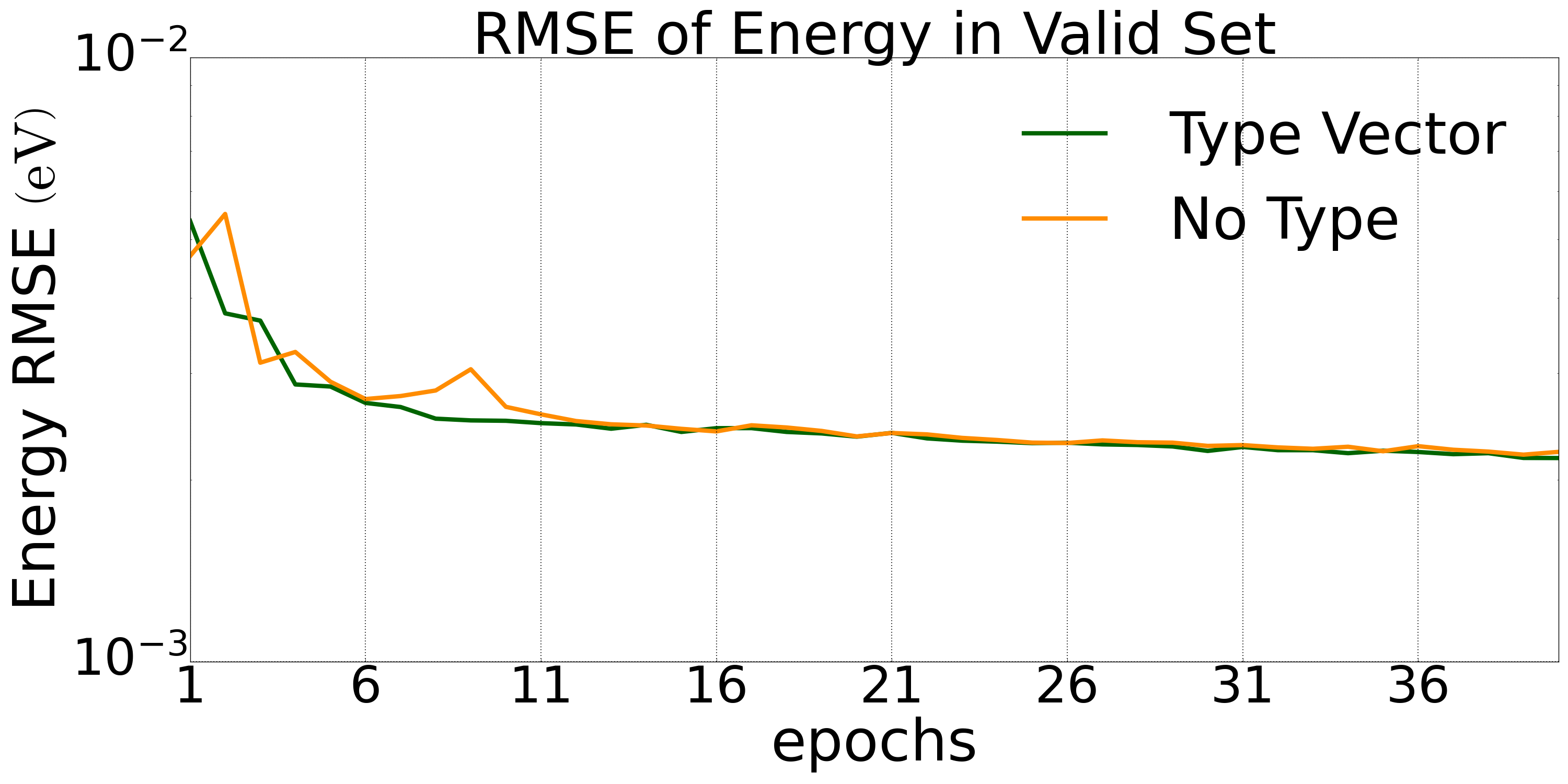图1: 四元LiGePS体系验证集上的能量误差下降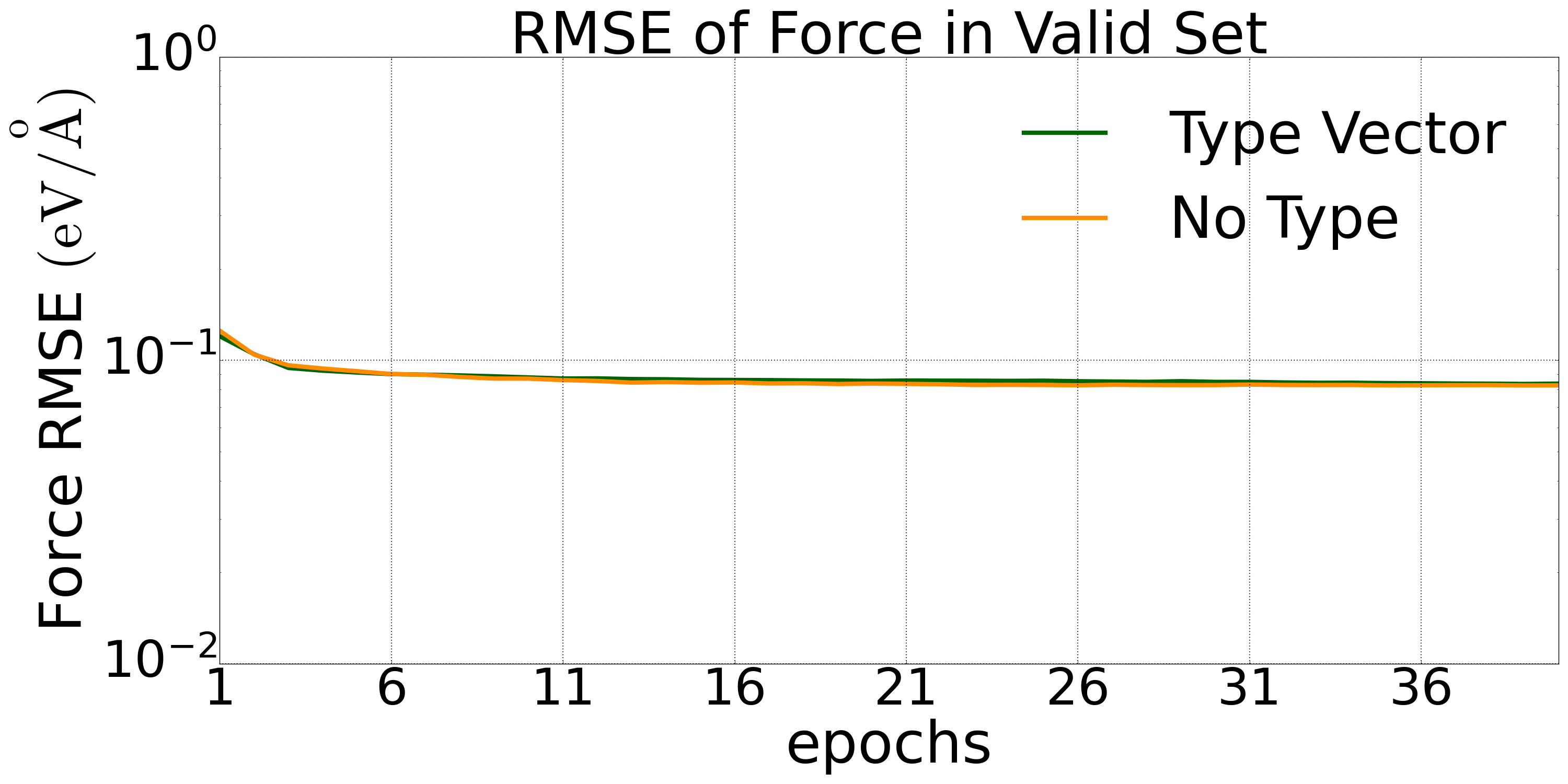

图2: 四元LiGePS体系验证集上的力误差下降

训练时间

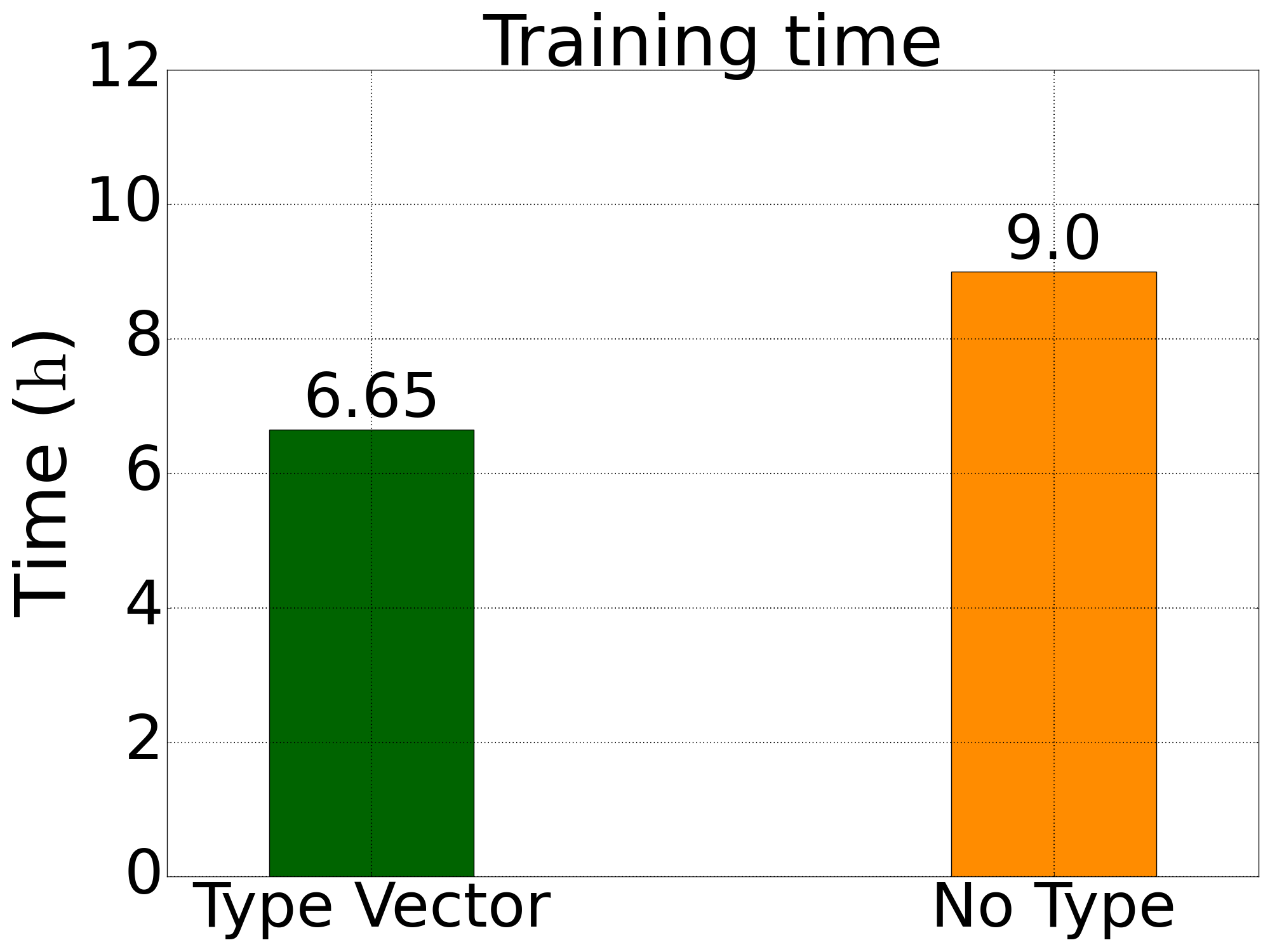图1: 五元合金体系训练总时间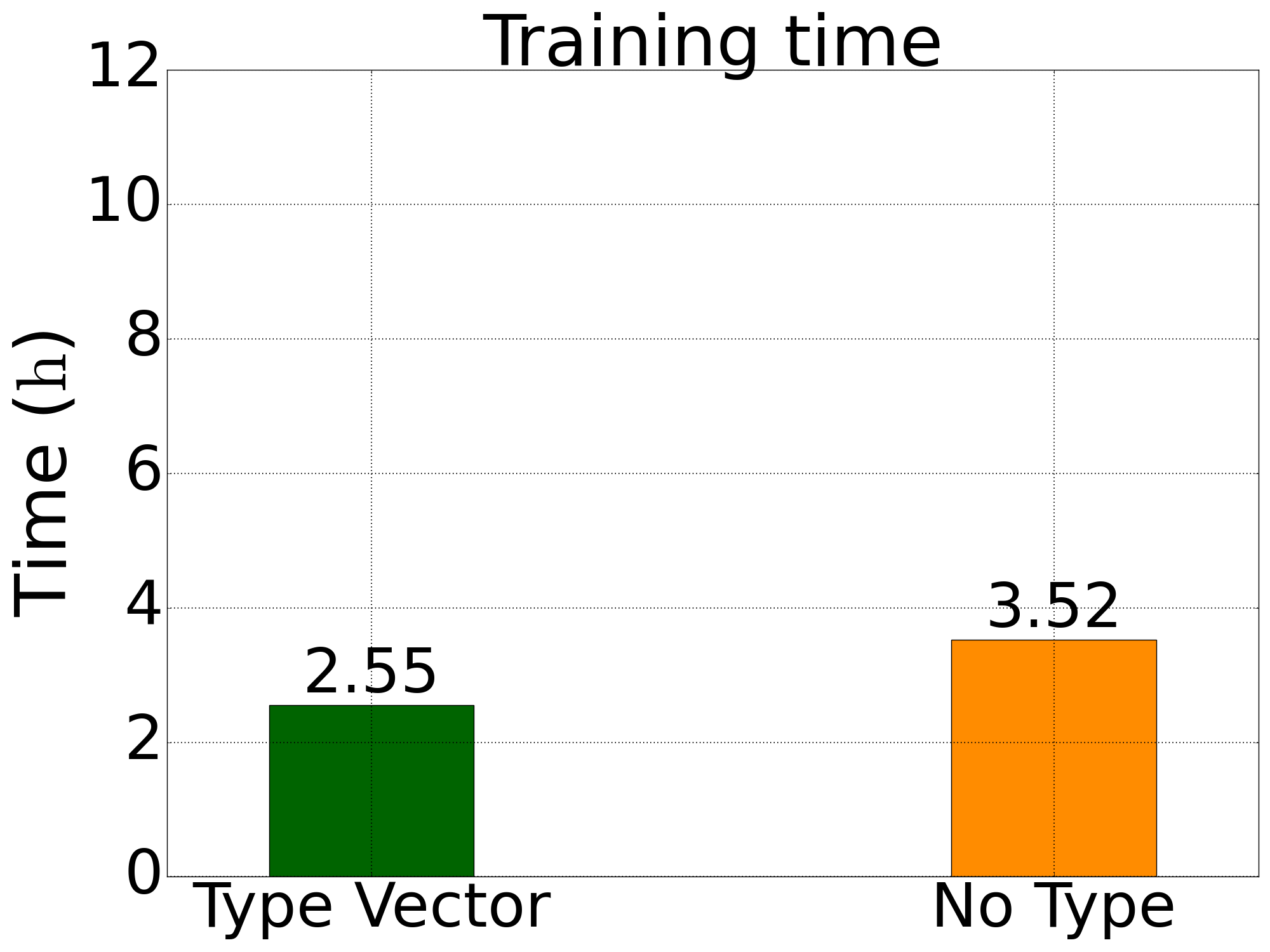

图2: 四元LiGePS体系训练总时间

在 Lammps 中的力场调用方式与前述标准的 DP 模型调用方法相同。

多项式模型压缩

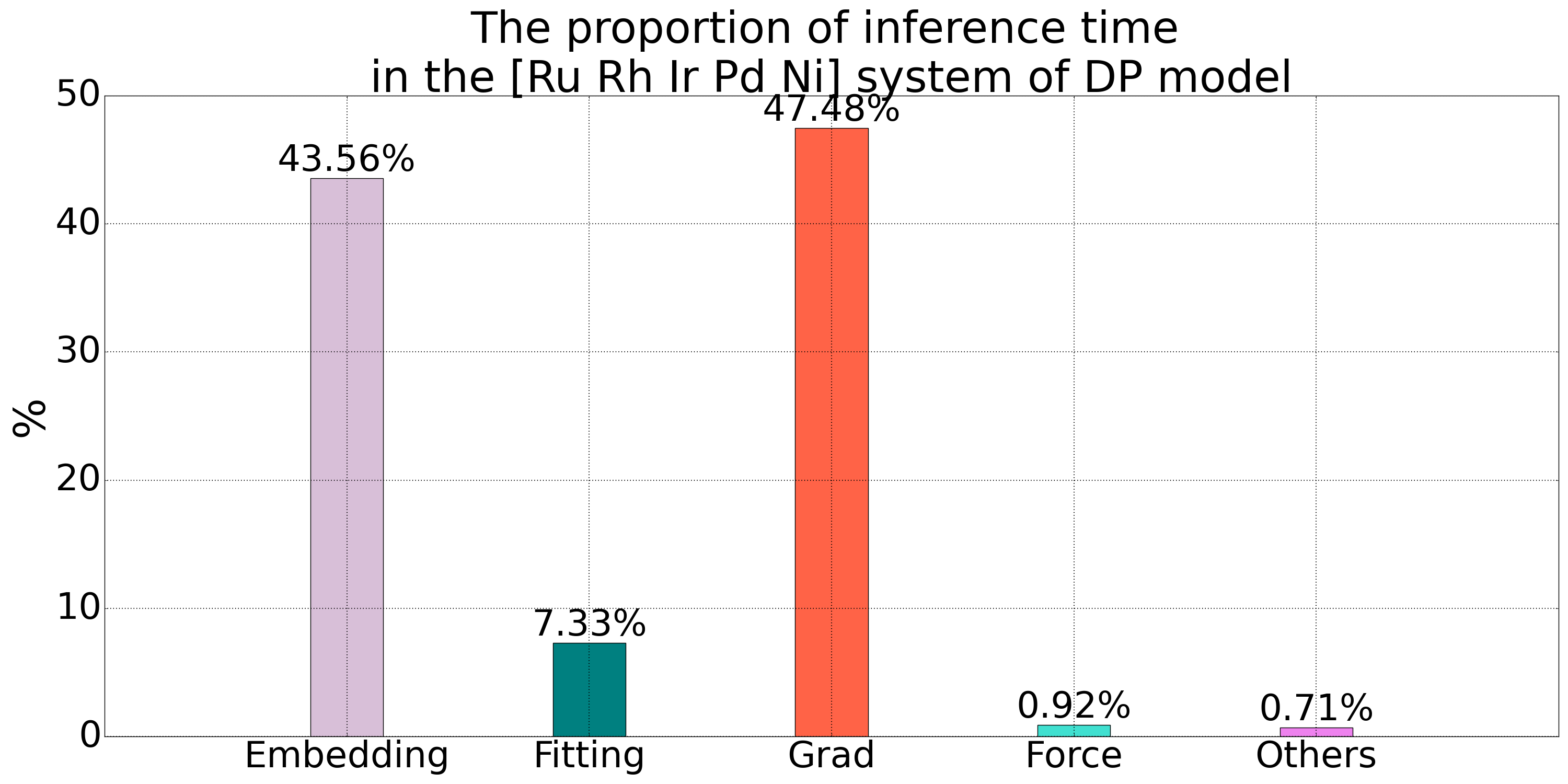
DP 模型的 Embedding net 网络数目是原子类型数目$N$的$N^2$倍，随着原子类型增多，Embedding net 数目会快速增加，导致用于反向传播求导的计算图的规模会增加，成为 DP 模型做推理的瓶颈之一。如下我们对于一个五元合金系统在 DP 模型的推理过程的时间统计所示，对于 Embedding net 计算以及梯度计算的时间占比超过 90%，这存在大量的优化空间。Embedding net 的输入为一个$S_{ij}$的单值，输出为$m$个值（$m$为 Embedding net 最后一层神经元数目）。因此，可以将 Embedding net 通过$m$个单值函数代替。

这里实现论文Lu D, Jiang W, Chen Y, et al. DP compress: A model compression scheme for generating efficient deep potential models中使用的五阶多项式压缩方法，同时我们也提供了基于 Hermite 插值方法的三阶多项式压缩方法供用户自由选择。

使用方法

对于一个训练后 DP 模型做模型压缩，完整的模型压缩指令如下：

PWMLFF compress dp_model.ckpt -d 0.01 -o 3 -s cmp_dp_model

• compress 是压缩命令
• dp_model.ckpt为待压缩模型文件名称，为必须要提供的参数
• -d 为S_ij 的网格划分大小，默认值为0.01
• -o 为模型压缩阶数，3为三阶模型压缩，5为五阶模型压缩，默认值为3
• -s 为压缩后的模型名称，默认名称为“cmp_dp_model”

模型压缩之后，在 lammps 中做分子动力学模拟使用方式与标准的DP 模型相同。

性能测试

模型压缩精度

我们在 Bulk 铜和五元合金体系上对 DP 模型做了模型压缩，并在测试集上分别做了测试。结果如下图中所示，对于铜体系，我们加入了对二阶插值方法的精度对比，相比于三阶和五阶方法，二阶方法的精度达不到要求。

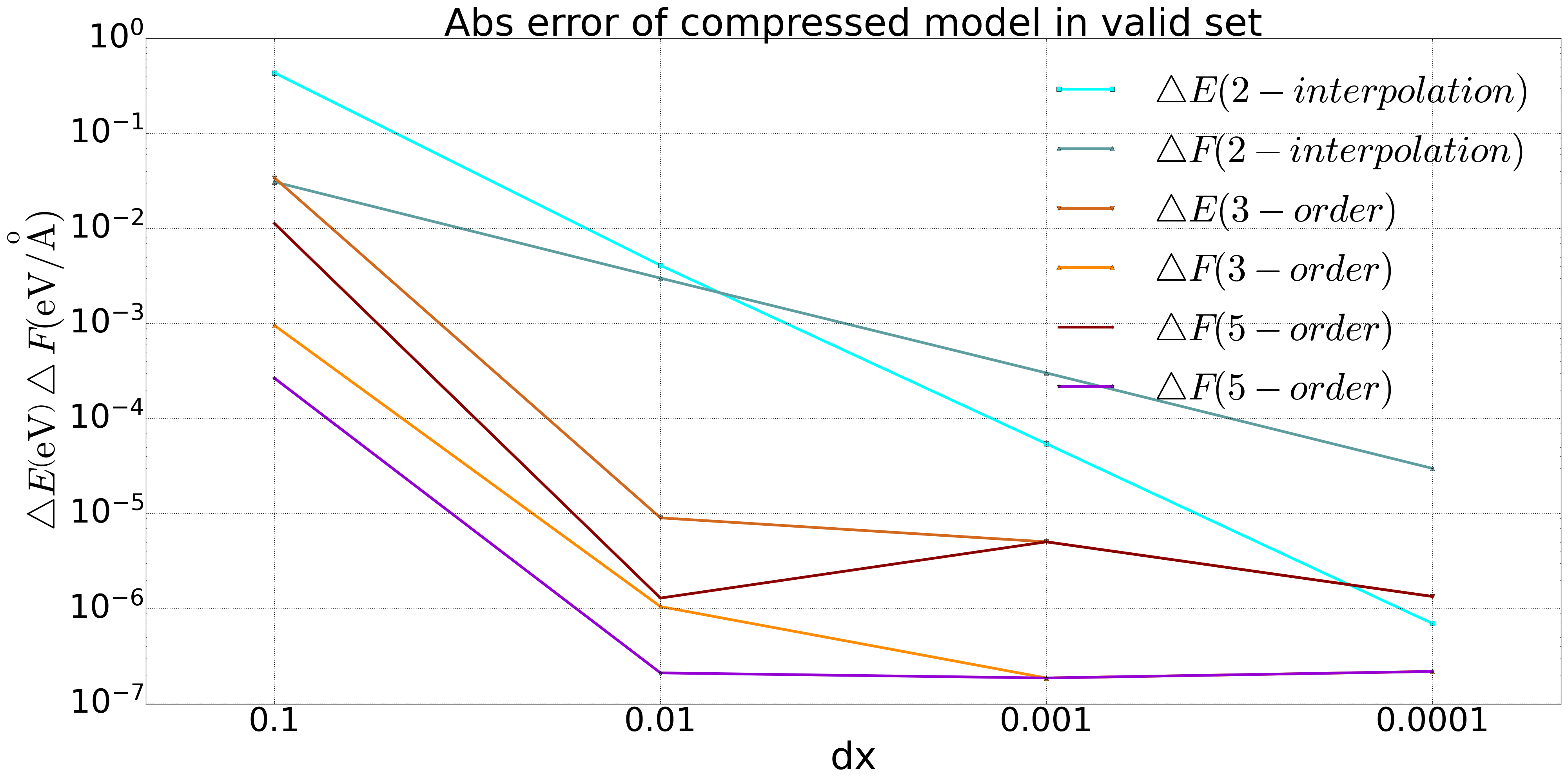图1: Bulk铜体系DP模型二阶、三阶与五阶多项式压缩对比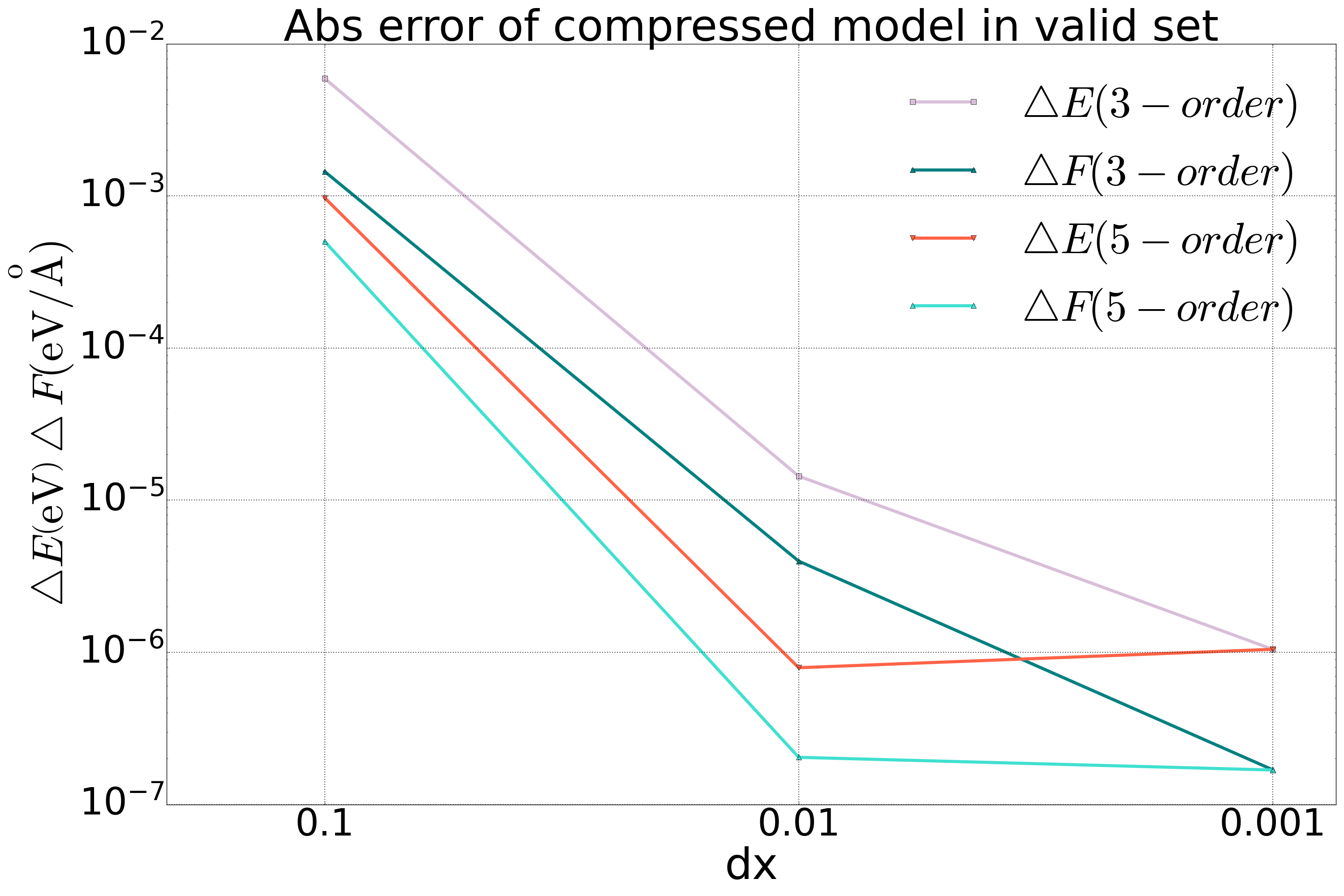

图2: 五元合金体系DP模型三阶与五阶多项式压缩对比

推理速度

我们统计了五元合金体系下 DP 模型三阶多项式压缩以及未压缩时，在整个测试集上的推理时间。经过多项式压缩后明显减少了反向求导（autograd）时间，这是因为多项式方法能够显著减少 Embedding net 在 pytorch 自动求导时的计算图大小。

图1: 五元合金体系三阶多项式压缩（dx=0.01）与未压缩对比

三阶多项式模型压缩过程

网格划分

我们扫描全部训练集，得到$s_{ij}$的最大值，由于$s_{ij}$是原子$i$和$j$的三维坐标距离$r_{ij}$函数，当$r_{ij}$ = $r_{cut}$时取最小值。根据$s_{ij}$取值范围按照$dx$值等分为$L$份，则共有$l+1$个插值点，分别记为$x_1,x_2,\cdots,x_l+1$。在实际的使用中，由于训练集的不完备，可能存在一些$s_{ij}$值超出训练集之外，这里我们在上述网格之外，继续增加了$s_{ij}$到$10\times s_{ij}$的网格，网格大小设置为$10 \times dx$。

三阶多项式

对于每个$[x_l,x_{l+1})$区间，采用如下的三阶多项式替代 Embedding net:

$$g^l_m(x)=a^l_mx^3 + b^l_mx^2 + c^l_mx + d^l_m$$

这里$m$为 Embedding net 最后一层神经元数量，即 Embedding net 输出值数目，多项式的自变量$x$值应为$s_{ij}-x_l$。在每个网格点上，都需要满足如下两个限定条件。 在每个网格点上限制如下条件。 多项式值与 Embedding net 输出值一致：

$$y_l = G_m(x_l)$$

多项式一阶导数与 Embedding net 对$S_{ij}$的一阶导一致：

$$y'_l = G'_m(x_l)$$

解得对应系数为

$$a^l_m=\frac{1}{\Delta t^3}[(y'_{l+1} + y'_l)\Delta t - 2h]$$ $$b^l_m=\frac{1}{\Delta t^2}[-(y'_{l+1} + 2y'_l)\Delta t + 3h]$$ $$c^l_m=y'_l$$ $$d^l_m=y_l$$

五阶多项式

我们也实现了DP Compress中的五阶多项式压缩方法。

对于五阶多项式，对$S_{ij}$的划分方法与五阶方法相同，采用如下的多项式代替 Embedding net： $g^l_m(x)=a^l_mx^5+b^l_mx^4+c^l_mx^3+d^l_mx^2+e^l_mx+f^l_m$

注意：此时多项式的自变量$x$值应为$s_{ij}-x_l$。在每个网格点上，都需要满足如下三个限定条件。

多项式值与 Embedding net 输出值一致： $y_l=\mathcal{G}_m(x_l)$

多项式一阶导数与 Embedding net 对$S_{ij}$的一阶导一致： $y'_l=\mathcal{G}'_m(x_l)$

多项式二阶导数与 Embedding net 对$S_{ij}$的二阶导一致： $y''_l=\mathcal{G}''_m(x_l)$

由此可得六个系数值分别为：

$a^l_m=\frac{1}{2\Delta t^5}[12h-6(y'_{l+1}+y'_l)\Delta t+(y''_{l+1}-y''_l)\Delta t^2]$

$b^l_m=\frac{1}{2\Delta t^4}[-30h+(14y'_{l+1}+16y'_l)\Delta t+(-2y''_{l+1}+3y''_l)\Delta t^2]$

$c^l_m=\frac{1}{2\Delta t^3}[20h-(8y'_{l+1}+12y'_l)\Delta t+(y''_{l+1}-3y''_l)\Delta t^2]$

$d^l_m=\frac{1}{2}y''_l$

$e^l_m=y'_l$

$f^l_m=y_l$

其中 $h=y_{l+1}-y_l$，$\Delta t=x_{l+1}-x_l$

model compression verification

model compress 方案，将$s_{ij}$取值范围分成$L$等份，则共有$l+1$个插值点，分别记为$x_1,x_2,\cdots,x_{l+1}$。对于每个$[x_l,x_{l+1})$区间，采用如下的五阶多项式替代 embedding network: $g^l_m(x)=a^l_mx^5+b^l_mx^4+c^l_mx^3+d^l_mx^2+e^l_mx+f^l_m$ 注意：此时多项式的自变量$x$值应为$s_{ij}-x_l$。在每个网格点上，都需要满足如下三个边界条件：

函数值一致

$y_l=\mathcal{G}_m(x_l)$

函数一阶导数一致

$y'_l=\mathcal{G}'_m(x_l)$

函数二阶导数一致

$y''_l=\mathcal{G}''_m(x_l)$

由此可得六个系数值分别为

$a^l_m=\frac{1}{2\Delta t^5}[12h-6(y'_{l+1}+y'_l)\Delta t+(y''_{l+1}-y''_l)\Delta t^2]$

$b^l_m=\frac{1}{2\Delta t^4}[-30h+(14y'_{l+1}+16y'_l)\Delta t+(-2y''_{l+1}+3y''_l)\Delta t^2]$

$c^l_m=\frac{1}{2\Delta t^3}[20h-(8y'_{l+1}+12y'_l)\Delta t+(y''_{l+1}-3y''_l)\Delta t^2]$

$d^l_m=\frac{1}{2}y''_l$

$e^l_m=y'_l$

$f^l_m=y_l$

其中 $h=y_{l+1}-y_l$，$\Delta t=x_{l+1}-x_l$